MECÂNICA GRACELI - QUÂNTICA TENSORIAL DE CAMPOS [592]

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

[

$\psi ^{*}$

$TeoriaInteraçãomediadorMagnitude relativaComportamentoFaixaCromodinâmicaForça nuclear forteGlúon10411/r71,4 × 10-15 mEletrodinâmicaForça eletromagnéticaFóton10391/r2infinitoFlavordinâmicaForça nuclear fracaBósons W e Z10291/r5 até 1/r710-18 mGeometrodinâmicaForça gravitacionalgráviton101/r2infinito$

Teoria	Interação	mediador	Magnitude relativa	Comportamento	Faixa
Cromodinâmica	Força nuclear forte	Glúon	1041	1/r7	1,4 × 10-15 m
Eletrodinâmica	Força eletromagnética	Fóton	1039	1/r2	infinito
Flavordinâmica	Força nuclear fraca	Bósons W e Z	1029	1/r5 até 1/r7	10-18 m
Geometrodinâmica	Força gravitacional	gráviton	10	1/r2	infinito

Na teoria quântica de campos, o intervalo de massa é a diferença entre a energia do vácuo e próximo menor estado de energia possível. A energia do vácuo pode ser definida por zero, e assumindo que todos estados de energia podem ser descritos como partículas em funções de onda, o intervalo de massa é a massa da partícula mais leve.

Já que a energia exata do valor próprio é infinitamente espalhada, logo excluída de uma descrição matemática formal, uma descrição mais apurada é que o intervalo de massa é a energia ínfima de qualquer estado que seja ortogonal em relação ao vácuo.

Definição

Para um dado campo real $\phi (x)$ , pode-se dizer que a teoria possui um intervalo de massa se uma qualquer de dois pontos possui a propriedade

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\langle \phi (0,t)\phi (0,0)\rangle \sim \sum _{n}A_{n}\exp \left(-\Delta _{n}t\right)

onde $\Delta _{0}>0$ é o menor valor energético no espectro do hamiltoniano, ou seja, é o intervalo de massa. Esta quantidade, facilmente generalizada para outros campos, é uma medida generalizada na teoria do retículo gauge. Isto foi matematicamente provado desta forma que pela teoria de Yang-Mills se desenvolve um intervalo de massa. O propagador terá a propriedade

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\lim _{p\rightarrow 0}\Delta (p)=\mathrm {constante}

sendo a constante finita. Um exemplo típico é oferecido por uma partícula massiva e livre, neste caso, a constante possui o valor $1/{m^{2}}$ . No mesmo limite, o propagador para a partícula sem massa será singular.

Exemplo

Um exemplo de intervalo de massa para teorias de partículas sem massa, pode ser visto na quebra espontânea de simetria ou no mecanismo de Higgs. No primeiro caso, tem-se que lidar com a aparência de excitações sem massa, Bóson de Goldstone, que são removidos pelo último caso devido a liberdade de gauge. A quantização preserva esta propriedade.

Um quark escalar sem massa pela teoria quântica de campos desenvolve um intervalo de massa de níveis clássicos. Então considere-se

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\Box \phi +\lambda \phi ^{3}=0.

esta equação possui a seguinte solução

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\phi (x)=\mu \left({\frac {2}{\lambda }}\right)^{\frac {1}{4}}{\rm {sn}}\left(p\cdot x+\theta ,-1\right)

onde $\mu$ e $\theta$ possuem integrais constantes e $� �$ é uma função elíptica de Jacobi, fornece

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

p^{2}=\mu ^{2}{\sqrt {\frac {\lambda }{2}}}.

Representação de Källén-Lehmann

Se a representação espectral de Källén-Lehmann se confirmar, neste estágio se excluiria as teorias de gauge, pois a função de densidade espectral pode ser descrita de forma simples com um espectro discreto com um intervalo de massa

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\rho (\mu ^{2})=\sum _{n=1}^{N}Z_{n}\delta (\mu ^{2}-m_{n}^{2})+\rho _{c}(\mu ^{2})

onde $\rho _{c}(\mu ^{2})$ é a contribuição das partículas do espectro. Neste caso o propagador terá a seguinte forma

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\Delta (p)=\sum _{n=1}^{N}{\frac {Z_{n}}{p^{2}-m_{n}^{2}+i\epsilon }}+\int _{4m_{N}^{2}}^{\infty }d\mu ^{2}\rho _{c}(\mu ^{2}){\frac {1}{p^{2}-\mu ^{2}+i\epsilon }}

sendo $4m_{N}^{2}$ aproximadamente o ponto inicial do setor de partículas. Agora, utilizando-se o facto que

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\int _{0}^{\infty }d\mu ^{2}\rho (\mu ^{2})=1

Obtém-se a seguinte conclusão para as constantes na densidade espectral

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

1=\sum _{n=1}^{N}Z_{n}+\int _{0}^{\infty }d\mu ^{2}\rho _{c}(\mu ^{2})

É importante enfatizar que esta representação ainda não foi comprovada numa teoria de gauge,

Quebra espontânea de simetria é um processo pelo qual um sistema simétrico passa, de forma espontânea, para um estado não simétrico. Este tipo de processo, incomum na natureza física, é vital para a compreensão do modelo padrão das partículas fundamentais, que é um dos mais importantes ramos da física moderna.

Definição

Para que uma quebra espontânea de simetria ocorra, deve necessariamente haver um sistema no qual existam diversos estados subsequentes com iguais probabilidades de ocorrer. Este sistema, como um todo, então é tratado como um sistema simétrico. Entretanto apenas um dos estados subsequentes deve ocorrer e toda a probabilidade dos inúmeros estados diversos é reduzida a zero, já que não há mais simetria. Então, é dito que a simetria do sistema foi espontaneamente quebrada.

Definição formal

Quando uma teoria é dita simétrica com respeito à um grupo simétrico, mas afirma que um elemento deste grupo é distinto, então uma quebra espontânea de simetria ocorreu, ou seja, pela teoria, não é necessário que se identifique o elemento e sim apenas que haja um elemento distinto.

Importância no modelo padrão

Ver artigo principal: Mecanismo de Higgs

Sem a quebra espontânea de simetria o modelo padrão prediz a existência de um determinado número de partículas. Entretanto, algumas destas partículas (os bosões W e Z, por exemplo) são preditos de não possuir massa, quando na realidade eles possuem massa. Esta era a maior falha do modelo até que o físico escocês Peter Higgs e outros propuseram, através do que ficou conhecido por mecanismo de Higgs, o uso da quebra espontânea de simetria para comportar massa nestas partículas. O mecanismo por sua vez prediz a existência de uma nova partícula, o bosão de Higgs. O bosão/bóson de Higgs foi detectado no LHC do CERN em Julho de 2012, com probabilidade maior que 5 sigmas de ser verdadeira tal identificação.

Uso na matemática

Gráfico conhecido por função potencial do chapéu mexicano.

Na matemática o uso mais comum da quebra espontânea de simetria é pelo uso da Função de Lagrange, a qual essencialmente indica como um sistema irá se comportar por meio de termos potenciais

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

(1)\qquad {\mathcal {L}}=\partial ^{\mu }\phi \partial _{\mu }\phi -V(\phi ).

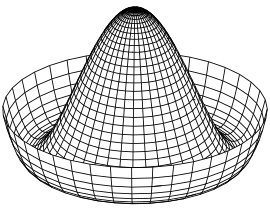
É neste termo potencial $V(\phi )$ que a ação da quebra de simetria ocorre. Como demonstra o gráfico do chapéu mexicano

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

(2)\qquad V(\phi )=-10|\phi |^{2}+|\phi |^{4}\,

Este termo potencial possui vários possíveis mínimos dados por

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

(3)\qquad \phi ={\sqrt {5}}e^{i\theta }

para qualquer real no intervalo $0<\theta <2\pi$ . Este sistema também possui um estado do vácuo quântico que corresponde ao $\phi =0$ , este estado possui um grupo unitário simétrico. Entretanto, uma vez que o sistema atinja um estado específico no vácuo (que corresponda a um valor para $\theta$ ) a simetria será espontaneamente quebrada.

Pesquisar este blog

MECÂNICA GRACELI - QUÂNTICA TENSORIAL DE CAMPOS [592]

Definição

Exemplo

Representação de Källén-Lehmann

Definição

Definição formal

Importância no modelo padrão

Uso na matemática

Comentários

Postar um comentário